*중간중간 생략한 내용이 있으니 참고바람
4. Algorithms
1) 검색 알고리즘
* Linear Search vs. Binary Search
[생각해보기]
Q. 만약 정렬되어 있지 않은 배열이 있다면 어떤 알고리즘이 더 빠를까?
A. 정렬되어 있지 않은 배열에는 이진 검색을 적용할 수 없기 때문에 이진 검색을 이용하는 것이 무의미하며 나아가 잘못된 값을 도출해낼 위험도 있다. 따라서 선형 검색을 이용하는 것이 더 효율적일 것이다.
2) 알고리즘 표기법

위와 같은 그림을 공식으로 표기한 것이 Big O 표기법입니다.
여기서 O는 “on the order of”의 약자로, 쉽게 생각하면 “~만큼의 정도로 커지는” 것이라고 볼 수 있습니다.
O(n) 은 n만큼 커지는 것이므로 n이 늘어날수록 선형적으로 증가하게 됩니다. O(n/2)도 결국 n이 매우 커지면 1/2은 큰 의미가 없어지므로 O(n)이라고 볼 수 있습니다.
주로 아래 목록과 같은 Big O 표기가 실행 시간을 나타내기 위해 많이 사용됩니다.
- O(n^2)
- O(n log n)
- O(n) - 선형 검색
- O(log n) - 이진 검색
- O(1)
Big O가 알고리즘 실행 시간의 상한을 나타낸 것이라면, 반대로 Big Ω는 알고리즘 실행 시간의 하한을 나타내는 것입니다.
예를 들어 선형 검색에서는 n개의 항목이 있을때 최대 n번의 검색을 해야 하므로 상한이 O(n)이 되지만 운이 좋다면 한 번만에 검색을 끝낼수도 있으므로 하한은 Ω(1)이 됩니다.
역시 아래 목록과 같은 Big Ω 표기가 많이 사용됩니다.
- Ω(n^2)
- Ω(n log n)
- Ω(n) - 배열 안에 존재하는 값의 개수 세기
- Ω(log n)
- Ω(1) - 선형 검색, 이진 검색
[생각해보기]
Q. 실행시간의 상한이 낮은 알고리즘이 더 좋을까요, 하한이 낮은 알고리즘이 더 좋을까요?
A. 상한이 낮은 알고리즘이 더 좋다. 언제나 최상의 경우로 실행되지는 않으며, 결과적으로 언제나 최악의 경우를 대비하여 평균적으로, 대체로, 실행시간이 낮은 알고리즘을 채택해야하기 때문에 상한이 낮은 알고리즘이 더 좋다.
4) Bubble Sort (버블정렬)

버블 정렬을 의사코드(pseudo code)로 나타내면 아래와 같다.

중첩 루프를 돌아야 하고, n개의 값이 주어졌을 때 각 루프는 각각 n-1번, n-2번 반복되므로 (n-1)*(n-2) = n^2-3n+2(n−1)∗(n−2)=n^2 −3n+2 번의 비교 및 교환이 필요합니다.
여기서 가장 크기가 큰 요소는 n^2 이므로 위와 같은 코드로 작성한 버블 정렬 실행 시간의 상한은 O(n^2)이라고 말할 수 있습니다.
정렬이 되어 있는지 여부에 관계없이 루프를 돌며 비교를 해야 하므로 위와 같은 코드로 작성한 버블 정렬의 실행 시간의 하한도 여전히 Ω(n^2)이 됩니다.
[생각해보기]
Q. 버블 정렬이 효율적인 경우는 어떤 경우인가요? 반대로 어떤 경우에 비효율적이게 될까요?
A. 데이터가 적고, 정렬되지 않은 배열의 경우 효율적일 것이다.
5) Selection Sort (선택정렬)
정렬을 위한 알고리즘 중 선택정렬을 배열 안의 자료 중 가장 작은 수(혹은 가장 큰 수)를 찾아 첫 번째 위치(혹은 가장 마지막 위치)의 수와 교환해주는 방식의 정렬입니다.
선택 정렬은 교환 횟수를 최소화하는 반면 각 자료를 비교하는 횟수는 증가합니다.
의사코드(pseudo code)로 나타내면 아래와 같습니다.

여기서도 두 번의 루프를 돌아야 합니다.
바깥 루프에서는 숫자들을 처음부터 순서대로 방문하고, 안쪽 루프에서는 가장 작은 값을 찾아야 합니다.
따라서 소요 시간의 상한은 O(n^2)이 됩니다. 하한도 마찬가지로 Ω(n^2) 입니다. 버블 정렬과 동일합니다.
[생각해보기]
Q. 선택정렬을 좀 더 효율적으로 어떻게 바꿀 수 있을까요?
A. 댓글들에는 최소값과 최댓값을 찾고, 그들을 제외한 최소값과 최댓값을 또 찾고 이를 반복하는 형태가 많이 제시되었다. 그러나 최솟값만 찾던 것이 최댓값까지 같이 찾아야되는 것으로 바뀌면, 한번 루프를 돌 때 계산을 두배로 해야한다. 결과적으로는 루프를 도는 횟수도, 계산량도 비슷하기 때문에 좋은 답은 찾지 못하겠다.
6) 정렬알고리즘의 실행시간
버블 정렬을 좀 더 잘 할 수 있는 방법을 알아보겠습니다.
만약 정렬이 모두 되어 있는 숫자 리스트가 주어진다면 어떨까요?
원래 의사코드는 아래와 같습니다.
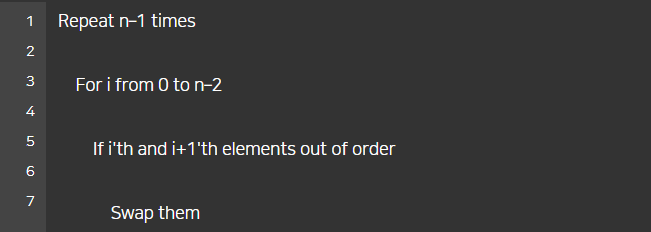
여기서 안쪽 루프에서 만약 교환이 하나도 일어나지 않는다면 이미 정렬이 잘 되어 있는 상황일 것입니다.
따라서 바깥쪽 루프를 ‘교환이 일어나지 않을때’까지만 수행하도록 다음과 같이 바꿀 수 있습니다.

따라서 최종적으로 버블 정렬의 하한은 Ω(n)이 됩니다.
상황에 따라서는 선택 정렬보다 더 빠른 방법이 되는 것이죠.
실행시간의 하한
- Ω(n^2): 선택 정렬
- Ω(n log n)
- Ω(n): 버블 정렬
- Ω(log n)
- Ω(1): 선형 검색, 이진 검색
[생각해보기]
Q. 선택 정렬의 실행 시간의 하한도 버블 정렬처럼 더 단축시킬 수 있을까요?
A. 최솟값을 매 루프마다 처음부터 끝까지 탐색하여 찾아야 하므로 불가능하다.
(n-1) + (n - 2) + 1 번 탐색하게 된다. 계산하면 n^2 - 2n + 1이므로 빅오 표기법으로 보면 실행시간은 Ω(n^2)이 된다. 즉, 방법적으로나 시간적으로나 변함이 없다.
7) Recursion (재귀)
함수를 사용할 때 어디에서 호출했나요? main 안에서 프로그램을 작성하면서 필요한 순간에 호출하여 사용합니다.
그런데 main 역시 함수라는걸 기억하시나요? main이라는 함수 안에서 또 다른 함수를 사용한 것입니다.
이 사실을 알게 되었을 때, 우리는 함수가 본인 스스로를 호출해서 사용할 수 있는지에 대해 의문을 가질 수 있습니다.
이에 대한 대답은 할 수 있다 이며, 이러한 것을 재귀(Recursion)라고 부릅니다.
아래와 같이 피라미드 모양을 출력하기 위해 다음과 같은 코드를 작성할 수 있습니다.
#
##
###
####
#include <cs50.h>
#include <stdio.h>
void draw(int h);
int main(void)
{
// 사용자로부터 피라미드의 높이를 입력 받아 저장
int height = get_int("Height: ");
// 피라미드 그리기
draw(height);
}
void draw(int h)
{
// 높이가 h인 피라미드 그리기
for (int i = 1; i <= h; i++)
{
for (int j = 1; j <= i; j++)
{
printf("#");
}
printf("\n");
}
}
바깥 쪽 루프를 없앤 draw함수를 만들고, 이를 ‘재귀적으로’ 호출하도록 해서 똑같은 작업을 수행할 수 있습니다.
즉, draw 함수 안에서 draw 함수를 호출 하는 것이죠. 아래 코드와 같이 수정할 수 있습니다.
#include <cs50.h>
#include <stdio.h>
void draw(int h);
int main(void)
{
int height = get_int("Height: ");
draw(height);
}
void draw(int h)
{
// 높이가 0이라면 (그릴 필요가 없다면)
if (h == 0)
{
return;
}
// 높이가 h-1인 피라미드 그리기
draw(h - 1);
// 피라미드에서 폭이 h인 한 층 그리기
for (int i = 0; i < h; i++)
{
printf("#");
}
printf("\n");
}
draw 함수 안에서 draw 함수를 다시 호출 하는 부분을 유의하시기 바랍니다.
h라는 높이를 받았을 때, h-1 높이로 draw 함수를 먼저 호출하고, 그 후에 h 만큼의 #을 출력합니다. 여기서 내부적으로 호출된 draw 함수를 따라가다 보면 h = 0인 상황이 오게 됩니다.
따라서 그 때는 아무것도 출력을 하지 않도록 하는 조건문을 추가해줘야 합니다.
이렇게 재귀를 사용하면 중첩 루프를 사용하지 않고도 하나의 함수로 동일한 작업을 수행할 수 있습니다.

[생각해보기]
Q. 반복문을 쓸 수 있는데도 재귀를 사용하는 이유는 무엇일까요?
A.
1. 코드를 재사용하여 효율적이고 편리하다
2. 코드가 간결해진다.
3. 스택 메모리를 사용하기 때문에 속도가 빠르다.
4. 더불어 상기 문제의 경우, 중첩 반복문을 사용했을 때에는 O(n^2)의 복잡도를 지녔다면, 재귀적 방법을 차용했을 때에는 O(n)의 복잡도를 지니게 되므로 보다 효율적인 알고리즘이라 할 수 있겠다.
8) Merge Sort (병합 정렬)
전화번호부의 분할 정복 탐색처럼 데이터를 반으로 나누어간다는 것과 공통점이 있는 방법인 병합 정렬(합병 정렬)이 있습니다.
병합 정렬은 원소가 한 개가 될 때까지 계속해서 반으로 나누다가 다시 합쳐나가며 정렬을 하는 방식입니다.
그리고 이 과정은 재귀적으로 구현되기 때문에 나중에 재귀를 학습하면 더 이해하기 쉽습니다.
아래는 의사코드(pseudocode)와 프로그램 작동과정입니다.
이렇게 나누어지고 합쳐지는 중간 단계의 배열을 임시로 저장하고, 함수가 종료될 때까지 기억하고 있어야하기 때문에, 메모리의 필요한 공간이 늘어납니다.

병합 정렬 실행 시간의 상한은 O(n log n) 입니다.
숫자들을 반으로 나누는 데는 O(log n)의 시간이 들고, 각 반으로 나눈 부분들을 다시 정렬해서 병합하는 데 각각 O(n)의 시간이 걸리기 때문입니다.
실행 시간의 하한도 역시 Ω(n log n) 입니다. 숫자들이 이미 정렬되었는지 여부에 관계 없이 나누고 병합하는 과정이 필요하기 때문입니다.

[생각해보기]
Q. 병합 정렬을 선택 정렬이나 버블 정렬과 비교했을 때 장점과 단점은 무엇이 있을까요?
A.
장점 : O(n^2)에서 O(nlogn)으로, 시간 복잡도가 크게 줄어든다.
단점 : 나누어지고 합쳐지는 중간 단계의 배열을 임시로 저장하고, 함수가 종료될 때까지 기억하고 있어야하기 때문에, 메모리의 필요한 공간이 늘어난다.
'TIL저장소' 카테고리의 다른 글
| [네이버 부스트코스]CS50 2019 모두를 위한 컴퓨터과학 6.데이터구조 (0) | 2021.06.28 |
|---|---|
| [네이버 부스트코스]CS50 2019 모두를 위한 컴퓨터 과학 5. 메모리 (0) | 2021.06.27 |
| [스파르타코딩클럽] 웹개발 4주차 flask서버, api설계 (0) | 2021.06.25 |
| [스파르타코딩클럽]웹개발 3주차 MongoDB/robo3T/pymongo/웹스크래핑(크롤링) (0) | 2021.06.22 |
| [스파르타코딩클럽] 웹개발 3주차 파이참 패키지 설치(bs4/requests)/웹스크래핑(크롤링)/DB설치(robo3t) (0) | 2021.06.22 |
